Kubikkmeterhuset 5.-10. Trinn Oppgave 9: Kvadrater på Skrå
Trinn: 5.-10.
Mål: Problemløsing med areal og brøk
Begreper: Areal, brøk, geometri, problemløsing
Utstyr: Papir og blant, ruteark eller kopier av kopieringsoriginal i tilknytning til denne oppgaven, saks
Oppgave
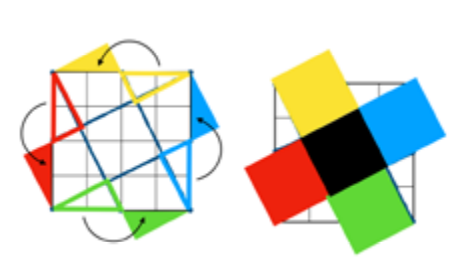
1. Tegn linjestykker fra hjørnene i kvadratet og til midtpunktene på sidene i kvadratet, som vist her, for å lage et mindre kvadrat i midten:
Hvilken brøk av arealet til hele kvadratet er arealet til kvadratet i midten?
Oppgaven er tidkrevende, gi elevene god tid, slik at de får muligheten til å finne gode løsninger. Oppgaven kan fungere som avslutning på flere timer, som en “ukas nøtt“.
TIPS: om enkelte elever bli stående fast, anbefales at de klipper ut delene langs de diagonale linjene og utforsker videre med delene.
2. Diskuter forskjellige løsningsstrategier og løsninger.
3. Ute på Kubikkmeterhuset kan elevene se en versjon av oppgaven. Dette kvadrat er delt i 100 desimeter kvadrater, hver er 1% av arealet til det hele. Be elevene om å bruke disse rutene for å finne andre måter å løse oppgaven på.
Løsning
Det fins mange måter å løse problemet på. Måtene er avhengige av elevenes nivå og verktøy. Her er flere løsningsmetoder (som elevene kan ha brukt).
Løsning med papirklipp:
Ved å klippe ut kvadrater langs diagonale linjer kan delene settes sammen for å lage 5 kongruente kvadrat. Et av dem er kvadratet i midten. Da er dette kvadratet 1/5 av arealet.
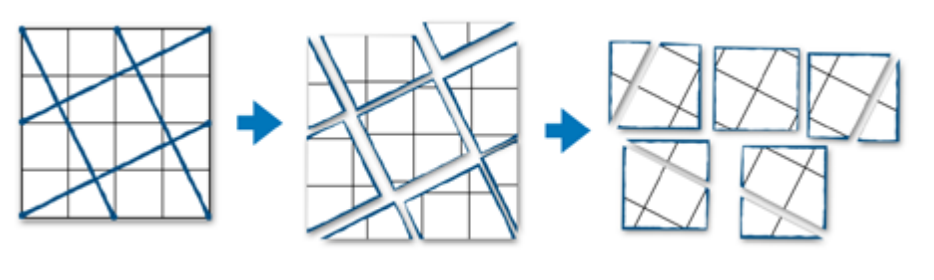
Løsning med mønster-utvidelse:
Ved å utvide designet kan vi lage et større kvadrat med hjørner hvor de diagonale linjene krysser vannrette/loddrette linjer. Da blir det lettere å finne og sammenligne arealene. Om vi setter sammen 3×3 designene, får vi et stort kvadrat. Da kan vi finne arealet ved å telle rutene og rettvinklede trekanter (som har areal 1 rute hver). Arealet av det store kvadratet er 80 ruter. Det store kvadratet består av 5×5 = 25 kvadrater på skrå som er størrelsen vi ønsker å finne i oppgaven. Hver har areal 80/25 = 3,2 ruter. Opprinnelig design er laget av 16 ruter. Da er brøken av arealet 3,2 : 16 = 0,2 … som er 1/5.
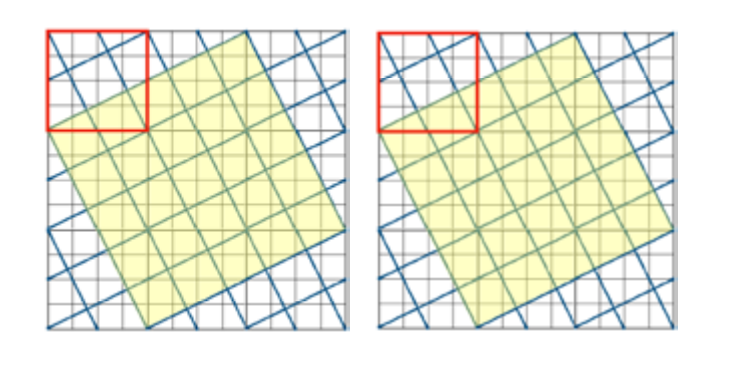
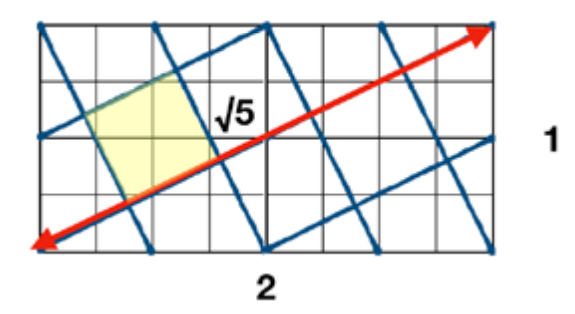
Løsning med Pytagoras setning:
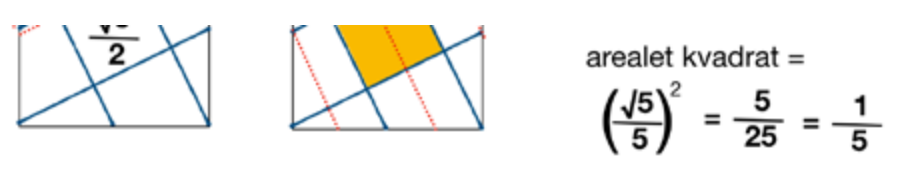
a) Sett sammen 2 kopier av designet for å lage et 1 x 2 rektangel. Diagonalen blir √5. Nøyaktig 5 kvadrater på skrå passer langs denne lengden, da er sidelengden √5 / 5, og arealet er (√5 / 5)2 = 1/5.
b) Lengden til en av de diagonale linjestykkene kan finnes uten å utvide designet som i (a). Finn hypotenusen til den rettvinklede trekanten med sidelengdene 1 og 1/2. Lengden blir √5/2. Ved hjelp av ekstra streker tegnet parallelle med de diagonale linjestykkene, kan vi se at sidelengden av kvadratet i midten er 2/5 av lengden av hele det diagonale linjestykket.
Løsning med rotasjon:
I stedet for å klippe ut delene, kan den samme ideen brukes ved å visualisere rotasjon av rettvinklete trekanter for å fullføre kvadratene. Hele designet blir til 5 kvadrater, da er den i midten 1/5 av arealet